I’ll make a bold claim here - that the best in-office sport is foosball!
Games are quick, usually 5-10 minutes, high-energy, and contained - there’s no chasing after escaped balls.
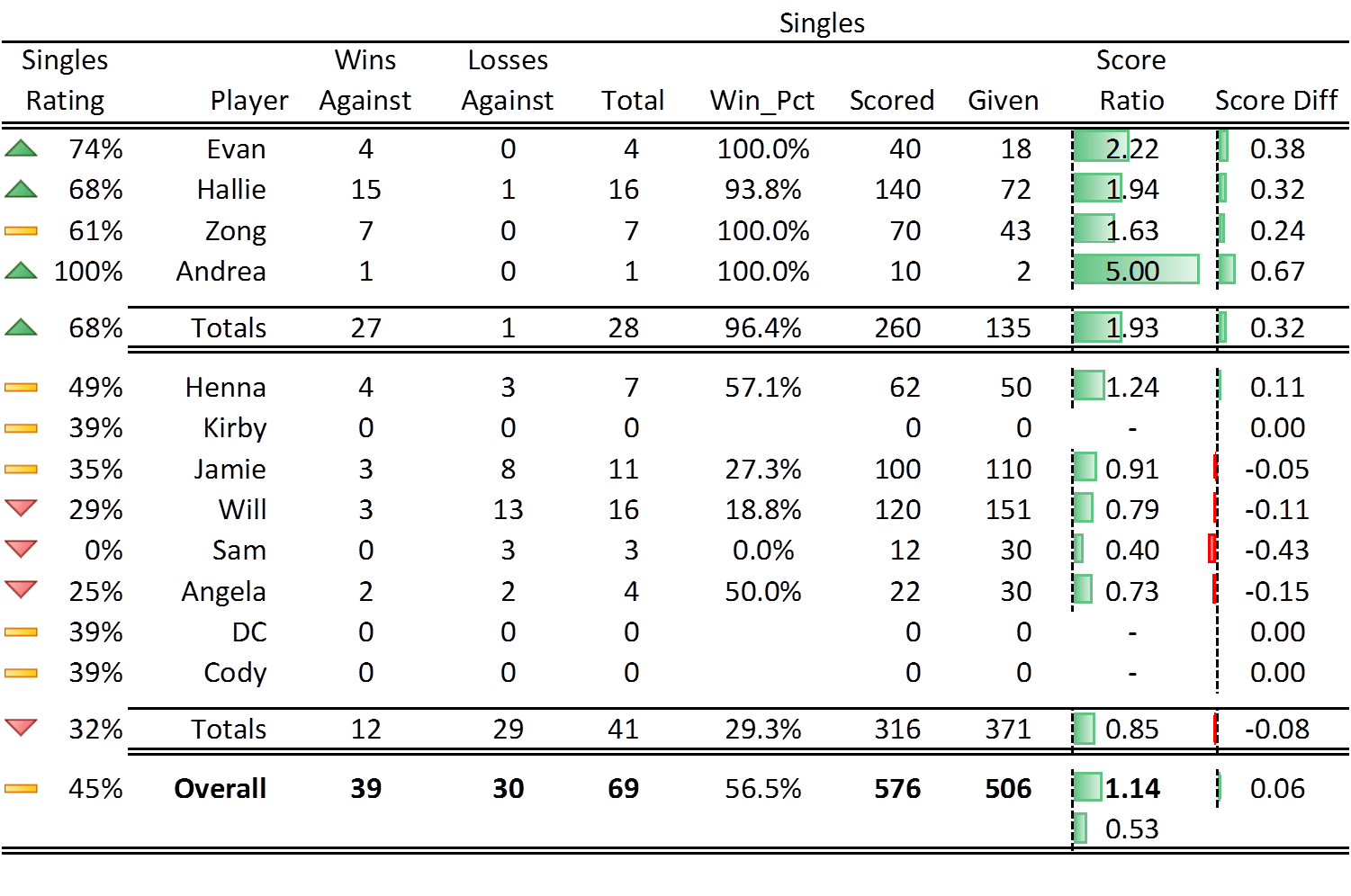
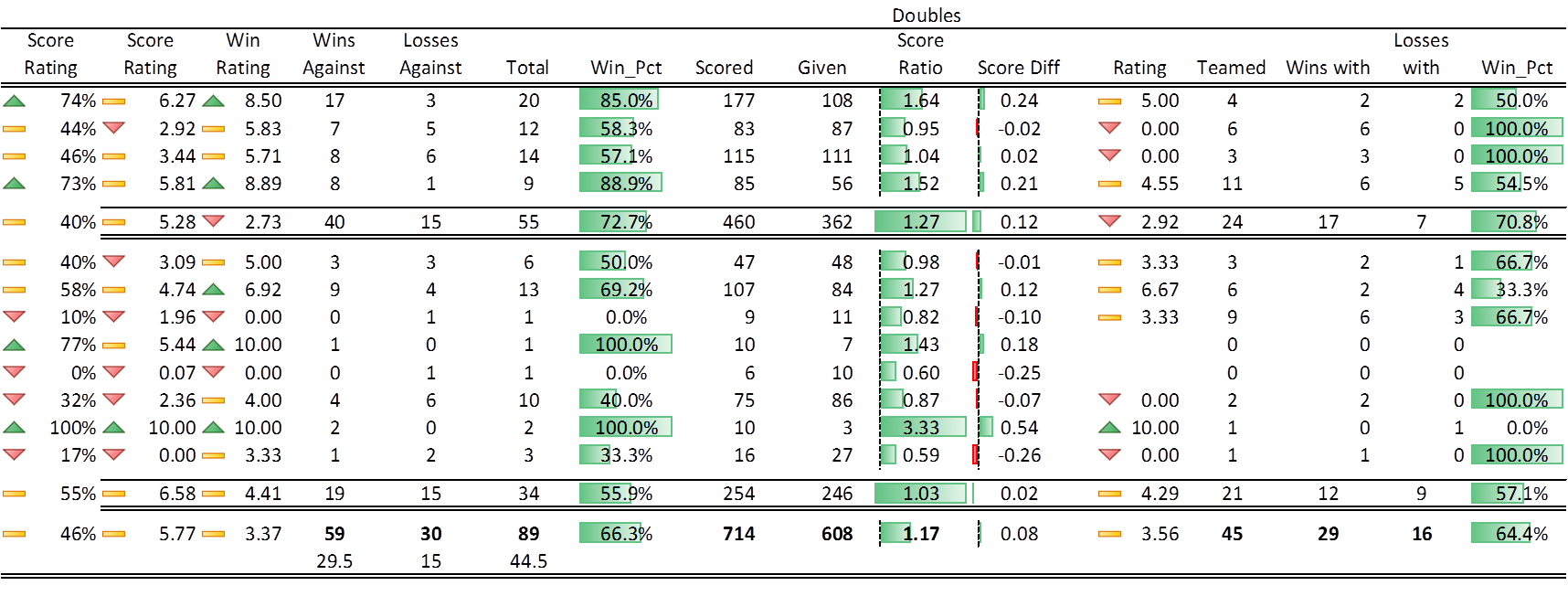
This analysis allows any player, singles or doubles, to add his or her scores via a short Google form.
The form feeds into an Elo-based ranking system hosted as a Shiny app, complete with a detailed analysis of other relevant statistics, such as expected matchup outcomes, player networks, win rates, and much more.
See it live here: Foosball Performance Analysis
Also fun is a fork of this Shiny App: Elo analysis applied to European Soccer Leagues
Elaborate backstory:
For my very first game in the SF Brattle office, I lost without scoring a point.
I decided I wanted to get better, and to do that, I wanted to measure my progress.
Thus, I created a score log of my personal games to rank myself compared to other my coworkers.
To tackle the issue that wins and losses were not directly comparable across people of different skill levels, I started off with a system of best-guess ratios.
This was a mess.
With some research, I found this was a fairly problem solved by the Elo ranking system, commonly used in head-to-head games like chess, soccer, football and basketball.
Details:
About Elo
The Elo rating system is a well-established method system for calculating relative skill of head-to-head competitors. It has been applied to chess, soccer aka football, basketball, American football, video games, Scrabble and more. These numbers are calculated based on some fairly simple rules.
A player’s Elo rating is represented by a number which increases or decreases depending on the outcome of games between rated players. After every game, the winning player takes points from the losing one. The difference between the ratings of the winner and loser determines the total number of points gained or lost after a game.
In a series of games between a high-rated player and a low-rated player, the high-rated player is expected to score more wins. If the high-rated player wins, then only a few rating points will be taken from the low-rated player. However, if the lower rated player scores an upset win, many rating points will be transferred.
A player whose rating is too low should, in the long run, do better than the rating system predicts, and thus gain rating points until the rating reflects their true playing strength.
Calculation applied here
The steps to the calculation are modified slightly to account for winning by a margin.
The margin of victory multiplier is based on Nate Silver’s NFL Elo system.
Here we use: MoV Multiplier = ln(abs(PD)) * (2.2/((ELOW-ELOL)*.001+2.2))
Where PD is the point differential in the game, ELOW is the winning player’s Elo Rating before the game, and ELOL is the losing player’s Elo Rating before the game.
Pitfalls
-
In the main set of calculations, players were not seeded with previous experience. The assumption that all players have an identical starting skill level is a poor one.
-
This unknown initial skill level is something that the Trueskill method by Microsoft tries to correct for.
-
Check out this discussion that describes some ways to adjust Margin of victory and account for some disadvantages of the system.